
Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
分析
题意是:爬一个n层的台阶,每一步可以迈1层或者2层台阶,要爬到台阶顶部,有多少种不同的方式?
这是个斐波那契数列问题。我们这样想,最后一步肯定是爬到台阶顶部的,那么这最后一步可以是从n-1层台阶上来的,也可以是从n-2层台阶上来的,因为一步可以迈1层或者2层。所以我们可以有递归公式f(n) = f(n-1) + f(n - 2),初始条件是f(0) = f(1) = 1.
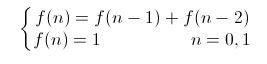
- 编程这个递归公式可以采用两种方法:递归式和非递归式。
- 递归式的编码方法直观、简单,缺点很明显,效率低,当n=38时,leetcode就给出了超时的错误
- 非递归式才能解决这道题目,使用循环实现。
Code
Code 1:递归式的解法(Limit Exceeded)
class Solution {
public:
/*
* 递归式的解法,当n比较大时,会超时,这里在n=38时,leetcode就报超时错误了。
*/
int climbStairs(int n) {
// Note: The Solution object is instantiated only once and is reused by each test case.
if( n ==1 || n == 0)
return 1;
return climbStairs(n - 2) + climbStairs(n - 1);
}
};Code 2:非递归式的解法(Accepted)
class Solution {
public:
int climbStairs(int n) {
// Note: The Solution object is instantiated only once and is reused by each test case.
if( n ==1 || n == 0)
return 1;
int lhs = 1, rhs = 1;
int temp;
for(int i = 1; i < n; i ++)
{
temp = lhs + rhs;
lhs = rhs;
rhs = temp;
}
return rhs;
}
};